The Clocks
Two clocks are designed identically such that if two photons simultaneously strike receptor cells attached to each clock, the clocks will stop. One, the station clock, is mounted above the tracks at a train station. The other, the train clock, is mounted such as to be in the exact center of an opened-top railcar on the train (by the train’s reference frame) when the moving railcar is centered about the station clock at 4:00-t (by the station’s reference frame).
The twin clocks are then sufficiently desynchronized so as to allow for them both to read exactly 4:00-t o’clock when the train passes the station and the clocks are transversely inline. This of course must be done considering the laws of relativity concerning the acceleration and speed of the train and the effect of that upon its clock. The alternative is merely to accomplish the simultaneity of the clock’s timing by trial an error.
The Flashers
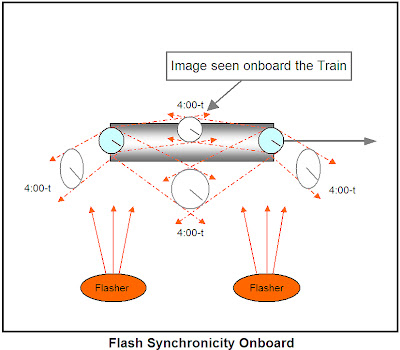
But in addition to the clocks, two photon flashers are mounted on the railcar walls, one on the front and one on the rear walls. Each photon flasher also has a clock identically timed to match the centered train clock at 4:00-t.
Also each flasher is set to fire 2 photons toward the center of the railcar at exactly 4:00 o’clock minus the calculated time for a photon to travel to a centered clock (t). The objective being to have the photons stop each clock at exactly 4:00 o’clock. So with each flasher, one of its photons is aimed slightly upward toward the receptor cell of the station clock and the other slightly downward at the same angle reversed to meet the receptor cell of the train clock.
If the railcar could instantaneously stop at 4:00-t, all four photons would strike a receptor cell at exactly the same time and at exactly 4:00 o’clock. But since the train doesn’t stop, a question comes to mind as to which clocks will be stopped by the simultaneous photon strikes and at what time.
All photons involved are sourced from two equally moving flashers at 4:00-t. The front flasher releases two identical photons that have no reason to travel at different velocities from each other. The back flasher photons similarly have no reason to travel at different velocities than each other. And none of the photons have any means to know of or vary due to being inside or outside of the railcar.
It is speculated that a photon, like a radio wave, travels independently of its source and thus all four photons must travel at the exact same velocity covering the exact same distance in the same amount of time and regardless of which direction the flashers were moving or which frame of reference is used to take the measurements as long as only one is used.
Relativity
Galilean invariance or Galilean relativity is a principle of relativity that states that the fundamental laws of physics are the same in all inertial frames and lead to Einstein’s Special and General relativity theories. What this principle means in this example is that no matter which frame of reference is used as the designated inertial frame to measure the paths of the photons (on the moving train or at the station) all four photons must be measured to travel the exact same distance over the same amount of time (t).
Relativity of Simultaneity
In this scenario, the flashers are already set to be identical and in sync at 4:00-t station clock time. Nothing comes from either frame to set them off as they have their own internal clocks, thus the relativity of simultaneity doesn't get involved and doesn't apply.
The simultaneity of the flashes is guaranteed for both frames due to the predesigned simultaneity through whatever means is necessary to ensure they flash at exactly 4:00-t as measured by both clocks and their internal clocks. Neither flasher has impetus to flash before the other from either reference frame. Thus both reference frames would see a simultaneous flash from the two flashers as by design, there is never an opportunity for the flashers to become asynchronous or misaligned with respect to either reference frame.
If you are one of the many who have become confused regarding relativity of simultaneity and believe that the Lorentz equations demand that the train and the station cannot both see the flashes as simultaneous, consider that such has merely been a misunderstanding of how to use the Lorentz equations. Einstein remarked that due to the time it took light to travel from different sources, one person might come to believe that two events were simultaneous even though they were not. And consider the following;
In the following pictorials, two trains are first shown traveling the distance ∆x in the time ∆t. A clock is tossed onto each train, then photo flashed ∆t time later. The image of the train’s clock faces are reflected from each clock displaying their time reading at that moment and seen by everyone regardless of their distance from the flash. Each person will see the image at a different time, but there is only one image to be seen.
In the third portion of the pictorial, the two train’s are combined into one, showing that each clock face will still show the same time to anyone.
But since there is only one image to be seen regardless of which clock face and that image is broadcast everywhere, on board the train, the same image is seen as the train's clocks readings.
So far, the flashers at the station have been used to produce the flash and thus light has traveled from the flashers to the train clocks. But the direction of the light from the light source hasn’t anything to do with the synchronicity of the clocks, so if we have the clocks flash their face image at that moment instead of the station flashers, we would get the same image.
It is clear that all, on board the train and off, will see the same image of the synchronized clocks on the train.
The flash timers mentioned in the paradox are clocks that flash at a given time setting, “4:00-t”. If they were to show their clock face as a flash, everyone would see the same image of “4:00-t” from both clocks whether on board the train or off. The train timers and clock are therefore synchronous in both frames. The question in the paradox isn’t what will be seen, but when it will be seen.
Summery of the Setup
To summarize the scenario setup, let me go through it again with less explanation.
A station clock is set so that at 4:00-t a railcar will be passing by. On that railcar, fore and aft, two flashers are set to go off exactly when the station clock will be reading 4:00-t and when they are equal distance from the station clock with respect to the station clock’s reference frame. So by design, both flashers trigger at exactly 4:00-t as indicated by the station clock.
Also aboard the train, a train clock is set to be exactly centered between the two flashers by its own reference frame when the station clock reads 4:00-t regardless of how the station reference frame might view it. The train clock is then adjusted so that it too will read exactly 4:00-t at that same moment.
Thus at 4:00-t as read by either clock, both flashers are designed to flash. Simultaneity of the flashing and centeredness of the clocks are guaranteed by setup design.
Station Reference Frame
If we examine the paths of the photons from the reference frame of the station, we can see that two photons would strike the station clock simultaneously and stop that clock at exactly 4:00 o’clock. But the train clock would be moving during the flight time of the photons (t) and thus would no longer be centered. Thus the train clock would not stop.
Train Reference Frame
But if we examine the paths of the photons from the reference frame of the moving train, we see that the two photons aimed at the train clock will strike simultaneously and thus stop the train clock at 4:00 o’clock. But the from the train’s reference, the station clock is moving in the backwards direction, thus the station clock, no longer being centered, would not stop.
The Paradox
When the train finally stops, each clock is examined to see if either has stopped running. This situation presents us with a paradox;
A) One clock has stopped – The speed of light is not constant for the other observer.
B) Both clocks have stopped – The speed of light is not constant for either observer.
C) Neither clock has stopped – The speed of light is dependent on an absolute frame.
Only One Clock Stopped
Since from either reference frame, the other clock is moving out of center, the principle of relativity requires that both reference frames must insist that their own still centered clock stops and that the other doesn’t. But since only one stopped, one of the reference frames did not measure the photon travel from fore and aft flashers to be equal. That means that either the principle of relativity, the consistency of the speed of light, or the simple logic of mathematics involved could not be true.
Both Clocks Stopped
Since the center distance from the flash was changing for both of the frames with respect to the other, only one could represent an equal distance and time of travel for the photons. That would imply that the photons inside the train behaved differently than those outside without having influence to do so.
Neither Clock Stopped
If neither clock stopped, from the perspective of both frames, light did not travel an equal distance in the same amount of time. This directly indicates that the speed of light is NOT constant for all observers, but rather has an absolute frame of reference of its own.
Light Dependency
If we temporarily speculate that perhaps a photon carries with it a portion of its source’s velocity, we can rebuild the scenario.
If a photon traveling from the back wall of the train were to travel a little faster because the train wall was moving, we must accept that the distance traveled by the two aft photons will be greater than those of the two forward photons over the same period of time. With this speculation in mind, we can simply reposition both clocks slightly more forward so as to align them with a simultaneous collision with their receptor cells. But in so doing, we run across the exact same paradox merely repositioned.
If for some odd reason photons carry a negative component of their source’s velocity, we could merely reposition the clocks slightly back from center so as to achieve simultaneous collision. But again, we run into that exact same paradox. Each clock must stop if examined by its own reference and not stop if examined from the other reference.
Thus we can remove the concern as to whether photons travel independent of their source, leaving us with;
Conclusion
If Galilean relativity is true, the speed of light is constant for any observer, and the logic of mathematics is true, then both clocks must stop and also not stop, yet each can be seen to either stop or not.
Relativity and Science are entirely embedded in the logic of mathematics. Thus if the logic of mathematics is to be dismissed, both Relativity and Science become useless, whether otherwise true or not. So that proposes that we have to accept that the speed of light is actually dependent on an absolute frame.
So we are left with no choice but to dismiss as a false or useless doctrine either the principle of Relativity and constant observed speed of light with all of its numerous consequential theories and calculations, or dismiss all of Science and the simplest mathematics. Take your pick or keep fantasizing. I choose to keep mathematics and Science and accept that indeed there really is an absolute frame of reference from which all things can be measured.
Einstein relativity down and out. Maxwellian aether back up for round two.







No comments:
Post a Comment