If you are not familiar with the Lorentz factor for time dilation, Wiki has an accurate article on it (warning: not everything in Wiki is).
Time is merely the measure of relative change but an accurate measure of it can be tricky. It has always been assumed that it doesn't matter in what manner something is changing, but merely how fast. The problem is that change comes with directions of change as an inherent property. Thus when someone speaks of traveling in a direction, the relative changing within the object involves that direction of travel.
The Lorentz transformation concerning time dilation for traveling objects assumes a photon bouncing between two mirrors. It is assumed that the speed of the light must be measured as the same for both an observer watching the traveling mirrors pass by as well as any observer on or in the traveling object. The issue is simply that the total distance of travel for the light will be perceived as different. The observer on the traveling object merely sees light bouncing directly up and down whereas the observer watching the object pass by sees that same light zigzagging up and down.
Speed is merely distance over time. And due to the presumption that light must be observed as traveling at the same speed regardless of one's travel and the distance being traveled is seen as different, the measurement of time itself must change in order to compensate the distance difference and yield the same speed. The Lorentz factor was derived merely by calculating a factor that would provide such compensation. And a reflecting photon was used to produce that factor. If the universe was made of bouncing photons, it would have been a good model.
But if one realizes that the universe is much more accurately modeled by spinning things rather than bouncing things, that compensating factor changes. In the following, I use a "square clock" to represent a spin rather than a round clock merely to simplify the mathematics. Whether round or square should not alter the compensation factor. What is important is that complete rotations are considered rather than linear reflections.
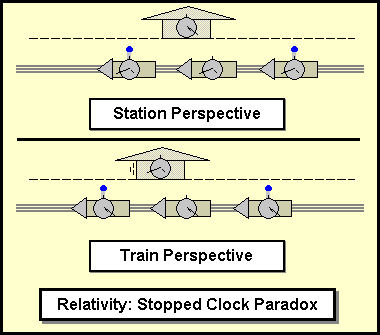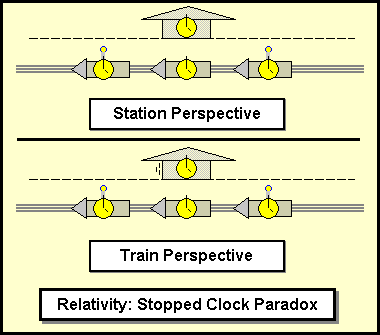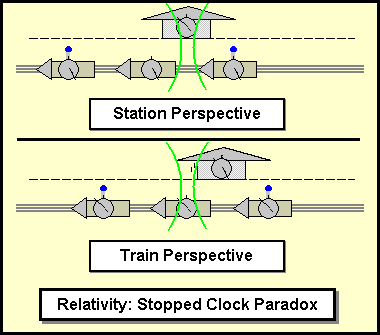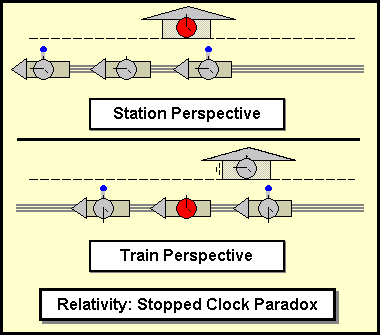
Fig 1. Square Clock versus Lorentz Clock
In figure 1, a comparison is made concerning the observed distance of travel for the photon in a linear light-clock and a square light-clock. The green dot represents a photon traveling. If the square clock is observed passing by and the speed of that photon is to be constant, one revolution of the traveling clock must take longer than a stationary clock would have taken. The same is true for the linear clock. But the dilation factors for the two types of clocks are different.
Linear, Lorentz Light-Clock Dilation Factor;
Square Light-Clock Dilation Factor;
But the story doesn't stop there. Note that the square clock is turning in one particular orientation with respect to its travel. All rotations aren't aligned to the direction of travel. And given any spaceship type of scenario, within the ship, particles and atoms will involve rotations in all three dimensions regardless of the direction of motion.
If a square-clock is facing the direction of travel, its dilation will be the same as the linear clock because there is no forward and back motion for the photon. And for any one direction of travel, two out of three orthogonal clocks will have square-clock dilation while one remains with linear dilation. Simply by taking the average of the dilation factors for each of the three directions so as to account for any direction of travel, we get;
Cubic Light-Clock Dilation Factor;
So for example, the Lorentz time dilation factor for an object traveling at 0.5 the speed of light is 0.8660. The Cubic dilation factor yields 0.8236 as a more accurate figure for real applications.
For extremely precise calculations, the exact method for measuring time must be considered.